Checklist voor een team:

• Gedisciplineerd handelen
• Gemeenschappelijk doel
• Eens over de resultaten
• Gemeenschappelijke aanpak
• Verantwoordelijk voor de resultaten
• Ontwikkelt een hoog niveau van elkaar aanvullende vaardigheden

Bron: Inspiratieboek coachen & presteren, Toon Gerbrands

Univariate analyse

Beschrijvingen van telkens één variabele worden ook wel univariate analyses genoemd. (...) Univariate beschrijvingen kun je op veel manieren maken. Wij behandelen er drie:

1. Frequentieverdelingen van een kenmerk: aanduiding hoe vaak een categorie (van een kenmerk) voorkomt in relatie tot het totale aantal cases.

2. Grafieken (plaatjes) van een kenmerk.

3. Kengetallen: vereenvoudigde beschrijving (samenvatting) van kenmerken op grond van één bepaalde eigenschap.

Ad (1) Frequentieverdelingen

De meest voorkomende manier van presenteren van variabelen is door aan te geven hoe vaak bepaalde scores voorkomen. Dit kun je doen met behulp van een frequentietabel. (...) Een frequentieverdeling kan er heel eenvoudig uit zien wanneer alleen informatie wordt gegeven over het aantal waarnemingen per categorie. Je kunt ook iets meer informatiegeven door de percentages van het totaal te berekenen. Zo ontstaat een relatieve frequentietabel.

(...)

Ad (2) Grafieken van één variabele

Om een goed beeld van een kenmerk te krijgen, maken onderzoekers vaak gebruik van grafieken. De keuze om een grafiek te maken hangt af van twee zaken: van je doel (wat wil je van een kenmerk laten zien) en van het meetniveau van het kenmerk.

(...)

Ad (3) Kengetallen

Met een kengetal geef je een samenvatting van een kenmerk door één bepaalde eigenschap ervan te benadrukken. Dat kun je doen door naar het midden (het centrum) van een verdeling te kijken. Je kunt ook kijken naar de breedte waarover de waarnemingen zich uitstrekken, de spreiding van een variabele. Er zijn dus twee soorten kengetallen, te weten centrum- en spreidingsmaten.

Bivariate analyses

De basis van de onderzoeksresultaten ligt bij het beschrijven van de onderzochte kenmerken. [Dit kan] van telkens één variabele worden gedaan, maar het is ook mogelijk om een beschrijving van twee variabelen tegelijk te geven, zoals inkomens van mannen en vrouwen, jaarcijfers van verschillende afdelingen, opleidingsniveau van mensen in bepaalde inkomenscategorieën, te veel om op te noemen. Naast kruistabellen (het weergeven van twee frequentieverdelingen in één tabel) kun je ook grafieken van twee variabelen gebruiken. Kijk er wel mee uit! Vergelijkingen tussen twee kenmerken zijn niet erg waardevol als je ze niet kunt toetsen. Wat wordt daarmee bedoeld? Welnu, je test of je de uitkomst van je analyses op een steekproef mag generaliseren naar de populatie. Dat kan alleen als de gevonden verschillen niet op toeval berusten. Hoe zeker moet je daarvan zijn? De meeste onderzoekers willen ten minste 95% zeker zijn dat de resultaten niet toevallig zijn.

Bron: Wat is onderzoek? Praktijkboek methoden en technieken voor het hoger onderwijs, Nel Verhoeven

The objective is not to take action, but to take meaningful action.

F. Kröger, M. Träm & M. Vandenbosch

Het grootste gevaar van teams is groupthink.

• De illusie van onkwetsbaarheid
• Denkbeeldige eensgezindheid
• Onderdrukte persoonlijke twijfel
• Afwijkende mening onder druk zetten
• Rationaliseren: verhalen waar ze zelf in geloven
• Ethische verbinding: eigen gelijk en eigen moraal
• Stereotypen: met een onscherpe blik naar anderen kijken

Bron: Inspiratieboek coachen & presteren, Toon Gerbrands

Mediaan

De mediaan is het middelste getal, als de getallen op grootte zijn gesorteerd. Een andere definitie van mediaan is de waarde waar 50% van de getallen vóór, en 50% van de getallen ná ligt. Als een groep van n getallen (een steekproef of een populatie) uit een oneven aantal bestaat, is de mediaan altijd gelijk aan het getal met rangenummer (n + 1)/2.

(...)

De mediaan van een even aantal waarnemingen is in eerste instantie niet te bepalen: er bestaat geen middelste waarneming. Daarom wordt de mediaan in een groep van n waarnemingen gedefinieerd als het (ongewogen) rekenkundig gemiddelde van de twee waarnemingen met rangnummers n/2 en (1 + n/2).

De mediaan

De mediaan is de waarde die hoort bij de middelste van de naar grootte gerangschikte waarnemingen.

Wanneer we een even aantal waarnemingen hebben, is er geen middelste waarneming; de mediaan is dan de waarde die ligt tussen de twee middelste waarnemingsuitkomsten. Het volgordenummer of rangnummer van de middelste waarneming vinden we door het aantal waarnemingen met één te verhogen en hiervan de helft te nemen.

(...)

Omdat de mediaan de waarde is van de middelste waarneming en dus de statische massa in twee gelijke delen verdeelt, kan de mediaan ook als volgt worden omschreven:

zowel onder als boven de mediaan, bevindt zich 50% van het aantal waarnemingen.

De mediaan is de middelste waarneming of díe categorie waarin de middelste waarneming voorkomt. De mediaan geeft precies het midden van een (gesorteerde) verdeling aan, de breuklijn ligt bij 50 procent. ... Toepassing van de mediaan kan vanaf een ordinaal meetniveau. ... De categorie waarin zich het 50^ste percentiel bevindt (zo noemen we de middelste waarneming), is de mediane categorie.

Bron:

• Statistiek voor de praktijk, R. Liethof & P van der Torre
• Basisboek kwantitatieve methoden - statistiek met exceltoepassingen, Donald van As & Jaap Klouwen
• Wat is onderzoek? Praktijkboek methoden en technieken voor het hoger onderwijs, Nel Verhoeven

Het gemiddelde wordt verkregen door alle scores bij elkaar op te tellen (de som dus) en vervolgens te delen door het aantal waarnemingen. Het wordt ook wel het rekenkundig gemiddelde genoemd. ... Een gemiddelde kan worden berekend voor variabelen vanaf een interval- of rationiveau. Waarom is dat? Een gemiddelde geeft pas informatie als je met de kenmerken ook daadwerkelijk kunt rekenen. Je kunt bijvoorbeeld zeggen dat de gemiddelde leeftijd van de mens tegenwoordig 85 jaar is. Maar je kunt niet zeggen dat de gemiddelde burgerlijke staat 'gehuwd' is. Er bestaat geen gemiddelde burgerlijke staat!

Bron:

• Wat is onderzoek? Praktijkboek methoden en technieken voor het hoger onderwijs, Nel Verhoeven

De modus is die categorie van een kenmerk die het meeste voorkomt. De modus kan worden toegepast bij variabelen vanaf een nominaal meetniveau; alle variabelen dus. ... Soms telt een verdeling niet één modus, maar twee. ... Deze verdeling wordt ook wel bimodaal genoemd, omdat ze twee toppen heeft.

De modus is de waarneming met de grootste frequentie. Deze centrummaat is vooral belangrijke bij kwalitatieve waarnemingen.

Bron:

• Wat is onderzoek? Praktijkboek methoden en technieken voor het hoger onderwijs, Nel Verhoeven
• Toegepaste statistiek - beschrijvende technieken, A.A.J. van Peet, G.L.H. van den Wittenboer & J.J. Hox
• Basisboek kwantitatieve methoden - statistiek met exceltoepassingen, Donald van As & Jaap Klouwen

Tabellen

Er zijn twee belangrijke mogelijkheden om gegevens te presenteren, namelijk tabellen en grafieken. ...

Door middel van een tabel kan men gegevens op een overzichtelijke wijze presenteren. Een tabel bestaat uit kolommen en regels. De doorsnijding van een kolom met een regel noemt men een veld. Een veld is daarmee een plaats in de tabel waarop een getal kan worden geplaatst.

Voor het opstellen van een tabel gelden enkele voorschriften. Er moeten aanwezig zijn:

• Een opschrift: boven iedere tabel moet in het kort aangegeven worden wat erin vermeld is. Dit opschrift moet kort en bondig zijn.
• Kolomkoppen: boven de kolommen van een tabel moet uit een zeer korte aanduiding blijken wat in die kolommen is weergegeven.
• Een voorkolom: in de voorkolom moet omschreven staan wat in de regels van de tabel is af te lezen.
• Logische volgorde: indien het mogelijk is, moet men de kolommen en de regels in een logische volgorde opstellen.
• Nummering: bij gecompliceerde tabellen is het nuttig om kolommen en regels te nummeren, zodat in de tekst een gemakkelijke verwijzing kan worden gemaakt naar een bepaald gedeelte van de tabel.
• Totalen: indien de getallen uit de tabel dit zinvol maken, dient men een kolom en/of een regel op te nemen met de totalen.
• ...
• Bronvermelding: indien de gegevens van de tabel uit een externe bron voortkomen, is het geven van een bronvermelding een vereiste. Ook als de gegevens binnen het bedrijf verzameld zijn, kan een bronvermelding nuttig zijn.

Bron:

• Statistiek om mee te werken, Arie Buys

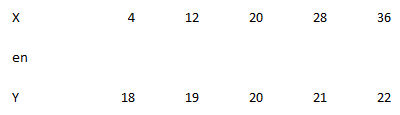
Stel, twee variabelen X en Y hebben de bovenstaande waarden.

Als we van X en van Y het gemiddelde uitrekenen, dan zien we dat dit in beide gevallen gelijk is aan 20. We zien echter ook dat de afwijkingen van de waarden op de variabele X tot het gemiddelde groter zijn dan bij Y: de verschillen bij X zijn groter dan bij Y. Klaarblijkelijk is het gemiddelde alleen onvoldoende om een serie scores te karakteriseren (te beschrijven). Behalve een centrummaat die aangeeft op welk deel van de schaal de scores liggen, is ook een maat nodig die aangeeft hoezéér de scores verschillen, dus hoever de scores afliggen van het centrum.

Een voor de hand liggend idee is om naar het verschil tussen de scores en het behorende gemiddelde te kijken, de zogenaamde afwijkingsscores (X - het rekenkundige gemiddelde). We zien dan hoever elke score van het centrum van de verdeling afligt. Het gemiddelde van deze afwijkingsscores lijkt in dit geval een mooie maat om iets over de spreiding te zeggen. ... Om de gemiddelde afwijkingsscores te bepalen, moeten we de afwijkingsscores optellen. We zien echter dat daar 0 uitkomt. De som van de afwijkingsscores ten opzichte van het gemiddelde is immers altijd 0. Maar dat betekent dat het gemiddelde verschil altijd 0 is en dat het dus niets zegt over de mate van spreiding. We moeten een andere oplossing vinden, willen we iets over de spreiding kunnen zeggen.

Bron:

• Toegepaste statistiek - beschrijvende technieken, A.A.J. van Peet, G.L.H. van den Wittenboer & J.J. Hox

Getrimd gemiddelde

Deze variant van het gemiddelde wordt als maatstaf gebruikt als twijfel is over de aanwezigheid van uitschieters in de steekproef. Men laat dan de kleinste en de grootste waarneming weg, of de kleinste en de grootste 2,5% van de waarnemingen en berekent het gemiddelde. Men noemt zo'n afgekapt gemiddelde het getrimde gemiddeld. Een andere naam waaronder men dit gemiddelde tegenkomt is modified mean.

Bron:

• Basisboek kwantitatieve methoden - statistiek met exceltoepassingen, Donald van As & Jaap Klouwen