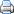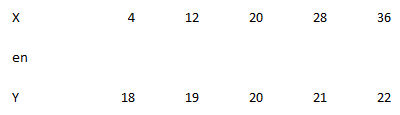
![]()
Stel, twee variabelen X en Y hebben de bovenstaande waarden.
Als we van X en van Y het gemiddelde uitrekenen, dan zien we dat dit in beide gevallen gelijk is aan 20. We zien echter ook dat de afwijkingen van de waarden op de variabele X tot het gemiddelde groter zijn dan bij Y: de verschillen bij X zijn groter dan bij Y. Klaarblijkelijk is het gemiddelde alleen onvoldoende om een serie scores te karakteriseren (te beschrijven). Behalve een centrummaat die aangeeft op welk deel van de schaal de scores liggen, is ook een maat nodig die aangeeft hoezéér de scores verschillen, dus hoever de scores afliggen van het centrum.
Een voor de hand liggend idee is om naar het verschil tussen de scores en het behorende gemiddelde te kijken, de zogenaamde afwijkingsscores (X - het rekenkundige gemiddelde). We zien dan hoever elke score van het centrum van de verdeling afligt. Het gemiddelde van deze afwijkingsscores lijkt in dit geval een mooie maat om iets over de spreiding te zeggen. ... Om de gemiddelde afwijkingsscores te bepalen, moeten we de afwijkingsscores optellen. We zien echter dat daar 0 uitkomt. De som van de afwijkingsscores ten opzichte van het gemiddelde is immers altijd 0. Maar dat betekent dat het gemiddelde verschil altijd 0 is en dat het dus niets zegt over de mate van spreiding. We moeten een andere oplossing vinden, willen we iets over de spreiding kunnen zeggen.
Bron: