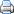A3 is
De A3-methode is een gestructureerde werkwijze voor het oplossen van problemen. Op een vel papier met A3 formaat, dwingt een strak sjabloon je om het probleem en de weg naar de oplossing helder en beknopt te formuleren. Feitelijk wordt je stap voor stap door een PDCA-cyclus geloodst. De titel van de A3 is een pakkende titel die aangeeft welke probleem gaat worden aangepakt. Nadat je het probleem duidelijk hebt, wordt je gedwongen eerst op zoek te gaan naar de diepere achterliggende oorzaken (root causes), voordat je in allerlei oplossingen schiet.
Plan
(1) Beschrijf de huidige situatie: wat is de achtergrond van het probleem? Wat doet er 'pijn'? Wat zijn de symptomen?
(2) Beschrijf het probleem: wat is de afwijking tussen de gewenste situatie en de huidige situatie (visueel, concreet)
(3) Formuleer de doelstelling: wanneer is het probleem opgelost? Wat is het beoogde resultaat of effect?
(4) Analyseer de grondoorzaken (5 x waarom)
(5) Definieer tegenmaatregelen: wat ga je doen om het probleem tegen te gaan en welke impact verwacht je hiervan? Hoe toets je of de tegenmaatregelen effectief zijn?
Do
(6) Experimenteer of de ingevoerde tegenmaatregel voor de bronoorzaak het verwachte resultaat weergeeft
Check
(7) Controleer of tegenmaatregelen effectief zijn: de mate waarin implementatie geslaagd is, bepaalt de aanbevolen/noodzakelijke vervolgacties (follow-up)
(8) Visueel maken
(9) Formuleer vervolgacties: als de doelstelling is gehaald kun je A3 afsluiten, als dit niet zo is, herzie dan de A3.
Act
Uitrollen van de tegenmaatregelen en definitief maken (incl. aantonen dat tegenmaatregelen blijvend functioneren).
Geneviève van Gemert maakte een handige instructie voor het maken van een A3.
Wil je zelf aan de slag, zie dan mijn mijn slidesharepresentatie Bluff Your Way Into A3-methode (voor probleemoplossing)

Zie ook:
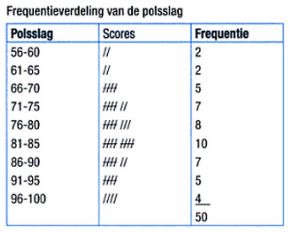
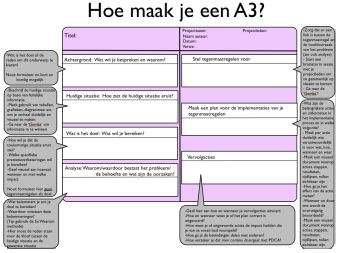
Een frequentie is het aantal malen dat een waarde van een variabele voorkomt. Door de aantallen te ordenen in een tabel of in een grafiek ontstaat een zogenaamde frequentieverdeling. Een grafiek waarmee een frequentieverdeling wordt weergegeven heet een histogram.
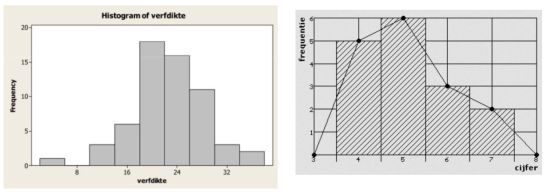
De oppervlakte van de kolommen in een histogram is gelijk aan de relatieve frequentie van de gegroepeerde waarden. In tegenstelling tot het klassieke staafdiagram sluiten in een histogram alle kolommen tegen elkaar. De middelpunten van de staven van een histogram worden soms met elkaar verbonden. De curve die door deze lijn wordt gevormd, wordt een frequentiepolygoon genoemd.
Bij het doen van onderzoek moet je als onderzoeker vaak zelfs de klassen bepalen. Door het gebruik van klassen treedt verlies van informatie op, maar daar staat tegenover dat er meer inzicht in de waarnemingen ontstaat. Als vuistregel voor het aantal klassen kies je door de wortel te nemen van het totaal aantal waarnemingen. De klassen hoeven niet allemaal even groot te zijn. Hoe groter de klassen, hoe meer informatie verloren gaat. Vaak worden voor gebieden waar weinig waarnemingen zijn, de klassen wat breder gemaakt.
De klassenbreedte is gelijk aan het verschil tussen de bovengrens van een klasse en de ondergrens van een klasse. Het aantal waarnemingen dat in een klasse valt, is de absolute frequentie. Wanneer je frequentieverdelingen met een verschillend aantal waarnemingen wilt kunnen vergelijk, kun je gebruik maken van de relatieve frequentie.

De laagste en hoogste waarde van de klasse noemen we de klassengrenzen. Klassen mogen elkaar niet overlappen. Het gemiddelde van de getallen die in een klasse kunnen voorkomen vormt het klassenmidden. Dit wordt ook wel gedefinieerd als de som van de onder- en bovengrenzen van een klasse, gedeeld door twee.
Wanneer er sprake is van ongelijke klassenbreedten, kun je de frequenties van waarnemingen niet direct vergelijken. Daarvoor zul je eerst de frequentie per gelijke eenheid moeten berekenen. Dit doe je door de frequentiedichtheid te berekenen, die onafhankelijk is van de gekozen klassenbreedte.

Door de frequentie van waarnemingen van verschillende klassen bij elkaar op te tellen, krijg je de cumulatieve frequentie.
Binnen Lean Six Sigma kun je een histogram gebruiken voor het visueel presenteren van data. Het doel van een histogram is het op een eenvoudige weergeven van de spreiding van gegevens. Door in het histogram ook de klantspecificaties op te nemen, zie je hoe het proces gecentreerd is rond de klantspecificaties en of de spreiding binnen de specificatielimieten valt. Het histogram geeft inzicht in de variatie in de data van een dataset en de ligging en geeft daarmee direct een indruk of het proces in staat is te voldoen aan de gestelde klanteisen ('procesprestaties').
Het histogram kan ook gebruikt worden om optisch te beoordelen of er sprake is van een normale verdeling. Bij een normale verdeling heeft het frequentiepolygoon een symmetrische klokvorm. Omdat de optische beoordeling subjectief is, is het vaak aan te bevelen om de gegevens weer te geven door middel van een normaliteitsplot (probability plot).
Om een histogram te maken, tel je de frequenties waarin de verschillende klassen (categorieën) voorkomen. Op de horizontale as geef je de relevante verdeling weer van de klassen. Elke klasse wordt vertegenwoordigd door een staaf ('balk'). Op de verticale as geef je de frequentie weer in absolute waarde of relatieve percentages. De hoogte van de weergegeven staven komt overeen met de frequentie van de betreffende klasse. Het is aan te bevelen een histogram alleen te gebruiken bij grotere datasets (tenminste 50-100 datapunten). Te kleine datasets leiden tot misleidende interpretaties. Als je meerdere pieken in het histogram ziet, kan de dataset te klein zijn of van meerdere metingen afkomstig. Als dat het geval is (her)overweg datastratificatie. Een 'gestratificeerd' histogram helpt om proceskenmerken te identificeren die mogelijk inzicht geven in mogelijke oorzaken van het probleem.

De frequentie (f) van een bepaalde gebeurtenis is het aantal keren dat de gebeurtenis is voorgekomen. De term gebeurtenis moet men hier zeer ruim nemen: het kan het verkrijgen van 'kruis' zijn bij het gooien van een munt, maar ook het vinden van iemand die in de klasse 'blond haar' valt, een proefwerkcijfer van een 7 gehaald heeft of een lengte tussen 170 en 179 heeft.
(...)
Een frequentieverdeling is een weergave van een aantal categorieën of klassen met de bijbehorende frequenties. Een frequentieverdeling is dus gebaseerd op de uitkomsten van een onderzoek. Het totaal aantal onderzochte personen (vaak aangeduid met de letter (n) dient onderaan de tabel te worden vermeld. Een frequentieverdeling kan weergegeven worden in een tabel, of in een figuur of grafiek. ... Veel gebruikte grafische vormen zijn het kolommendiagram, taartpuntdiagram en staafdiagram die alle gebruikt worden voor kwalitatieve gegevens als haarkleur, beroep, en dergelijke; voor het weergeven van numerieke gegevens gebruikt men het histogram, het stamdiagram en de frequentiepolygoon.

Frequentieverdelingen
Wanneer we een groot aantal gegevens hebben verzameld ten behoeve van een bepaald onderzoek dan is het doorgaans noodzakelijk dat deze gegevens nader bewerkt worden. Het op overzichtelijke wijze presenteren van deze gegevens is hierbij belangrijk. Om personen die niet betrokken zijn geweest bij het onderzoek een idee te geven van de resultaten, is het vaak nuttig om de gegevens te verwerken in een tabel of een grafiek.
Op deze manier kan een zeker overzicht van de betrokken variabelen verkregen worden, waardoor het patroon van de gegevens tot uiting komt. Voordat van een hoeveelheid 'losse' gegevens een tabel of een grafiek vervaardigd kan worden, is het noodzakelijk deze te ordenen.
Hierbij wordt de verzameling van mogelijke uitkomsten verdeeld in een aantal intervallen of groepen, die we klassen zullen noemen. Het in een klasse verdelen van het totale bereik van de variabele noemt men het maken van een klasse-indeling.
(...)
Bij het maken van een correcte klasse-indeling moet erop gelet worden dat rekening gehouden wordt met alle mogelijke uitkomsten van de betrokken variabele. Voor elke uitkomst moet een plaats zijn. Anderzijds moet ervoor gewaat worden dat er geen overlappingen plaatsvinden waardoor een bepaalde uitkomst in meer dan één klasse thuishoort. Een klasse-indeling die alle mogelijkheden overdekt maar geen overlappingen kent, noemen we een categorisch systeem.
Zodra er een dergelijke indeling in klassen gemaakt is, kan er 'geturfd' worden. Op deze manier kan worden vastgesteld hoe vaak er een waarneming behorend tot een bepaalde klasse verricht is. Het aantal waarnemingen in een bepaalde klasse noemt men de frequentie. De verdeling die aldus voor de klassen ontstaat, noemt men een frequentieverdeling.
(...)
Relatieve frequeties
... Nadat er een indeling in klassen tot stand is gekomen, kunnen de waargenomen uitkomsten geteld worden. Hierdoor ontstaan absolute frequenties. De som van de frequenties is uiteraard gelijk aan het totaal aantal waarnemingen.
Wanneer we de frequentie per klasse delen door het totale aantal waarnemingen, ontstaan relatieve frequenties. Relatieve frequenties kunnen van belang zijn bij het vergelijken van verschillende frequentieverdelingen.

Frequentieverdeling
De frequentie is het aantal keren dat een verschijnsel voorkomt. Bijvoorbeeld: er deden 20 mannen en 40 vrouwen mee aan het onderzoek. Als je alle frequenties in een tabel zet, heb je een frequentieverdeling. Het doel van de frequentieverdeling is om de resultaten van het onderzoek overzichtelijk weer te geven. We onderscheiden vier soorten frequentieverdelingen:
- ongegroepeerde frequentieverdeling
- gegroepeerde frequentieverdeling
- relatieve frequentieverdeling
- cumulatieve frequentieverdeling
Ongegroepeerde frequentieverdeling
Een ongegroepeerde frequentieverdeling wordt gebruikt wanneer van een variabele slechts weinig waarden voorkomen, zoals bij de vraag ‘Wat is uwleeft ijd?’ in een klas propedeuse-studenten van een hbo-instelling. Als van een variabele veel verschillende waarden voorkomen, is een ongegroepeerde frequentieverdeling niet overzichtelijk; zodra een variabele meer verschillende waarden kan aannemen, neemt de overzichtelijkheid van de tabel af.
(...)
Gegroepeerde frequentieverdeling
Als een variabele veel voorkomende waarden heeft en de waarde in groepen kan worden ingedeeld, ligt het voor de hand om te kiezen voor een gegroepeerde
frequentieverdeling.
Bij een gegroepeerde frequentieverdeling zet je de frequentie van een groep in een tabel. De frequentie van een groep of klasse is het totaal van de frequenties
van de afzonderlijke waarden die tot een bepaalde klasse behoren.
Als je bijvoorbeeld aan 150 verschillende mensen in een supermarkt hebt gevraagd ‘Wat is uw leeftijd?’, is de kans groot dat je veel verschillende
waarden hebt. In deze situatie ligt het voor de hand om de waarden in
klassen in te delen, zoals in tabel 8.3.
(...)
Relatieve frequentieverdeling
Als je groepen wilt vergelijken, kun je de relatieve frequentieverdeling nemen. Bij een relatieve frequentieverdeling laat je de frequenties van de verschillende klassen als een percentage zien.
(...)
Cumulatieve frequentieverdeling
De cumulatieve frequentieverdeling geeft het totale aantal frequenties weer dat zich onder een bepaalde klassengrens bevindt. Je telt als ware de frequenties tot dan toe bij elkaar op. Je doet dit om te weten welk deel van een verdeling onder een bepaalde waarde ligt. De meting moet wel op minstens ordinaal niveau zijn. Je zet de vragen in de rijen en de antwoordmogelijkheden in de kolommen van een tabel.
(...)
Ook is het mogelijk om een kruistabel te maken, waarin meerdere variabelen tegenover elkaar staan. Door de resultaten in een kruistabel te zetten, wordt het verband tussen de variabelen zichtbaar.
De onafhankelijke variabele zet je in de kolommen, de afhankelijke in de rijen. Verticaal percenteer je tot 100%, zodat je gemakkelijk kunt vergelijken. Daarna kun je met een chi-kwadraattoets onderzoeken of het verband tussen de variabelen significant is.
Zie ook: LSS: Probability Plot (normaliteitsplot)
Bron: