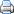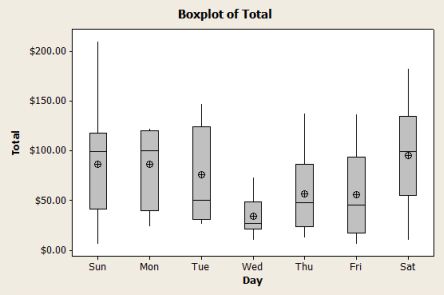
De kenmerken van een verdeling worden vaak samengevat door middel van het zogenaamde vijf-getallenresumé. Het vijf-getallenresumé wordt gevormd door respectievelijk:
-
De laagste uitslag in de gegevens.
-
Het eerste kwartiel (Q1, 25ste percentiel: een kwart van de waarnemingen ligt beneden deze score).
-
De mediaan, waarbeneden de helft van de waarnemingen valt.
-
Het derde kwartiel (Q3, 75ste percentiel).
-
De hoogste uitslag.
Het vijf-getallenresumé kan grafisch worden weergegeven in een boxdiagram (box plot). De Engelse benaming hiervoor is box-and-wisker plot, letterlijk doos-met-snorharen plaatje.
In een boxplot geldt:
-
De onder- en bovenkant van de box liggen bij de kwartielen, zodat de lengte van de box gelijk is aan de interkwartielafstand. De box bevat dus de helft van alle waarnemingen; de breedte van de box zegt niets; die is altijd hetzelfde.
-
De mediaan wordt in de box aangegeven door en streep.
-
De lijnenboven en onder de box (de 'snorharen') lopen tot de grootste en kleinste waarneming. Beneden de onderrand van de box bevindt zich dus het kwart van de gevallen met de laagste waarden; boven de bovenrand het kwart met de hoogste waarden.
Het centrum, de spreiding en het totale bereik van de verdeling zijn uit de boxplot direct te herkennen. Als de mediaan in het midden van de box ligt en als de snorharen niet even lang zijn, duidt dit op een scheve verdeling.
Bron: Statistiek in woorden, Anke Slotboom