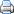Een belangrijke regelmatige verdeling is de binomiale verdeling. Het gaat daarbij om een variabele met maar twee waarden (raak en mis, kop of munt, vandaar het voorvoegsel 'bi') waarbij er een bepaalde kans op succes is. De binomiale verdeling beschrijft hoe groot de kans is dat een bepaald aantal observaties een bepaald aantal treffers oplevert. Als het aantal observaties naar oneindig nadert, benadert de binomiaal verdeling een normaal verdeling; eigenlijk is de normale verdeling ontdekt door het construeren van binomiale verdelingen. Op die manier beschouwd is de binomiale verdeling dus de moeder aller verdelingen....

Belangrijk om te onthouden is dat bij een binomiale verdeling altijd sprake is van een vast aantal pogingen n en een succeskans p per poging. Bij een Poisson-verdeling is dat niet het geval en daarmee is ook meteen het belangrijkste verschil tussen deze twee verdelingen aangegeven.

Veel verschijnselen of uitkomsten van experimenten zijn in te delen in één van de twee klassen: kruis/munt, man/vrouw, geslaagd/gezakt, introvert/extravert, je treft iemand thuis of niet, enzovoort. Men noemt een proces dat slechts tot twee mogelijke uitkomsten kan leiden, een Bernoulli proces.

Aan elk van de klassen is een kans verbonden: bij een zuivere munt is de kans op kruis gelijk aan de kans op munt, is 0,5; als 20% van de Nederlanders introvert is tegen 80% extravert, is de kans 0,20 dat een willekeurige Nederlander die je op straat aanspreekt, introvert zal zijn. De klasse waarin men geïnteresseerd is, wordt algemeen aangeduid met 'succes'; de bijbehorende kans wordt aangegeven met p.

Als ik nu een steekproef van tien willekeurige Nederlands aanspreek, zullen daarbij dan twee introverten zitten? Hoe groot is de kans dat het er drie zijn? Of vier? Minder dan twee? (...) De binomiale verdeling is een wiskundige regel voor het berekenen van de kansen op dergelijke uitkomsten. Het is dus een kansverdeling, die de kansen op respectievelijk 0,1, 2, ...., n successen geeft in een steekproef van n waarnemingen.

Voor het berekenen moeten n (de steekproefgrootte) en p (de kans op succes) bekend zijn. Deze grootheden heten de parameters van de binomiale verdeling.

Zie ook: LSS: Binomiale verdeling

Bron:

• Theorieboek Lean Six Sigma - upgrade to Blackbelt, Marco A.M. Koet (MKPC)
• Statistiek in woorden, Anke Slotboom