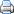![]()
Het Griekse symbool voor ? (sigma) wordt in de statistiek gebruikt als maat voor spreiding en wordt veelal de standaardafwijking (standaarddeviatie) genoemd. Veel kwaliteitsproblemen zijn gerelateerd aan de spreiding in kwaliteitskenmerken. Als immers een kenmerk veel variatie heeft rond zijn streefwaarde, zal dit kenmerk regelmatig tot buiten de toleratie- of specificatiegrenzen variëren.
De variatie van veel kwaliteitskarakteristieken kan beschreven worden met de zogenaamde normale verdeling. De normaalkromme geeft de relatieve frequentie weer waarmee een zekere kwaliteitsmetriek een bepaalde waarde aanneemt.
De waarde die het vaakst wordt aangenomen is tevens de gemiddelde waarde µ (mu). In de bovenstaande figuur zijn de streefwaarde en de specificatiegrenzen voor het kenmerk aangegeven. In eerste instantie gaan we ervan uit dat de gemiddelde waarde van het kenmerk samenvalt met zijn streefwaarde.
We zien dat het kwaliteitskenmerk zo nu en dan een waarde zal aannemen die buiten de specificatiegrenzen (LSL, USL) ligt. Indien deze grenzen op een afstand van drie keer de standaardafwijking (3?) vanaf de streefwaarde liggen, gebeurt dit met een frequentie van ongeveeer 0,27%. Indien de spreiding van dit kenmerk kleiner wordt, zal de standaardafwijking misschien wel vier keer tussen de specificatiegrenzen en de streefwaarde passen (4?). Het percentage buiten specificatie wordt dan 0,0063%. Met andere woorden: hoe groter de afstand tussen de streefwaarde en de specificatiegrenzen (in veelvouden van ?), des te beter presteert het proces. Een '3?'-proces produceert meer uitval dan een '4?'-proces. We zien dat het Sigma-niveau een maat is voor het aantal gebrekkige producten die een proces produceert (hoe hoger het Sigma-niveau, des te beter presteert het proces).
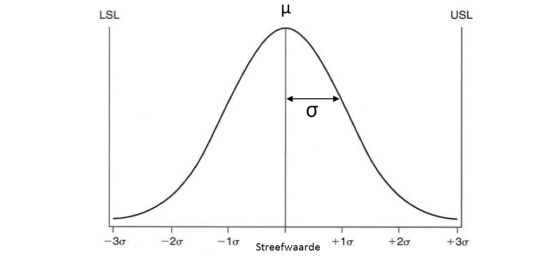
Het is een gegeven dat een kenmerk gemiddeld niet precies op de streefwaarde zit. Over een langere periodeeeee van productie zal het gemiddelde fluctueren rond de streefwaarde. Om hiervoor te corrigeren wordt er vaak vanuit gegaan dat het gemiddelde tot maximaal 1,5 x ? afwijkt van de streefwaarde.
Het aantal defecte producten dat een 3?-proces dan produceert, is fors groter, namelijk 6,7%. Deze berekening - die corrigeert voor een verschuiving van het gemiddelde ten opzichte van de streefwaarde van 1,5? - wordt het lange-termijn-Sigma-niveau genoemd. De onderstaande tabel geeft voor een aantal Sigma-niveaus het corresponderende uitvalspercentage en de opbrengst weer.
| Sigma-niveau | Uitvalpercentage | Opbrengst |
| 1? | 69% |
31% |
| 2? | 30,9% | 69,1% |
| 3? | 6,7% | 93,3% |
| 4? | 0,62% | 99,38% |
| 5? | 0,023% | 99,977% |
| 6? | 0,00034% |
99,99966% |
Door de relatie te gebruiken tussen Sigma-niveaus en uitvalspercentages (zoals weergegeven in de tabel) kunnen we het Sigma-niveau algemener toepassen en ook gebruiken als een maat (of 'metriek') voor processen die zich niet gedragen volgens de normale verdeling.
Bron: Six Sigma - stap voor stap, Ronald J.M.M Does, Jeroen de Mast