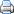
Regressie-analyse is een statistische techniek voor het onderzoeken van het causale verband tussen variabelen. Het onderzoek is erop gericht te analyseren in welke mate een verandering in één of meer variabelen leidt tot een verandering in een andere variabele. Het doel is het verklaren of voorspellen van een bepaalde variabele op basis van één of meerdere andere variabelen. Er wordt een lineaire relatie verondersteld tussen de afhankelijke (te voorspellen of te verklaren) variabele Y en een (of meerdere) onafhankelijke variabele X. Deze lineaire relatie kan worden uitgedrukt in termen van een regressievergelijking.

Regressie-analyse is nauw verwant met correlatieonderzoek. Beide technieken onderzoeken het verband tussen twee variabelen. Bij regressie ga je een stap verder dan bij correlatie. Je probeert aan de hand van de ene (onafhankelijke) variabele de veranderingen in de andere (afhankelijke) variabele statistisch te voorspellen, waarbij een regressievergelijking wordt opgesteld. Bij een correlatieanalyse is er geen duidelijke onafhankelijke variabele. Je wilt onderzoeken óf er een mogelijk verband bestaat tussen twee variabelen en hoe sterk dit verband is. De variabelen zijn 'gelijkwaardig'. Hét verschil tussen correlatie en regressie is statisch relevant, maar wordt in de praktijk niet zo strikt gehanteerd. Wanneer het doel van een onderzoek is een variabele te voorspellen uit de andere, spreekt men gewoonlijk over regressie. Is het doel slechts een index te geven van de mate van samenhang tussen twee variabelen, dan spreekt men van correlatie.

Associatie en correlatie zijn twee termen voor samenhang of afhankelijkheid tussen variabelen. Twee variabelen zijn afhankelijk, als de kans op een uitkomst op de ene variabele afhankelijk is van de uitkomst op de andere variabele. We spreken meestal van associatie, als de samenhangende variabelen discreet zijn, en van correlatie, als de variabelen continu zijn. Erg consequent wordt aan deze terminologie echter niet vastgehouden. Voor het bepalen van een samenhang is het belangrijk om vast te stellen op welk niveau de variabele gemeten is. Alleen wanneer beide variabelen op hetzelfde niveau zijn gemeten is er een samenhang te berekenen. Regressie-analyse maakt gebruik van het rekenkundig gemiddelde. Daarom moeten beide variabelen minstens interval meetniveau hebben. Ook mogen de variabelen geen extreme waarden hebben, aangezien zij de richting van de regressielijn sterk kunnen beïnvloeden in een kleinedata-set (van enkele tientallen waarnemingen).

Formeel spreek je spreek van associatie bij variabelen op nominaal/ordinaal meetniveau en over correlatie bij variabelen op een interval/ratio meetniveau. Je spreekt dus strikt genomen alleen van correlatie als twee continue variabelen samenhangen of afhankelijk zijn. De uitkomsten kan je weergeven in een spreidingsdiagram. De sterkte van een (lineaire) correlatie meten we met een correlatiecoëfficiënt (r), waarbij de waarde altijd ligt tussen -1 en +1. Correlatie tussen twee variabelen wil nog niet zeggen, dat de verschijnselen, die door die variabelen worden gemeten, een causaal verband hebben. Soms berust het geheel op toeval en men spreekt dan wel van een schijncorrelatie (pseudo-correlatie).

De aard van de relatie tussen continue variabelen kan worden samengevat in één getal, de correlatiecoëfficiënt (r). De officiële naam is Pearson product-moment correlaticoëfficiënt (pmcc) en de kortste weergave hiervoor is rxy (r van relatie, x en y als verkorte aanduiding van de beide variabelen). Bij het karakteriseren van het verband tussen variabelen zijn er drie aspecten waar je op kunt letten:

1. Aanwezigheid: is er een systematisch, statistisch significant verband, tussen twee variabelen (zie: sterkte).

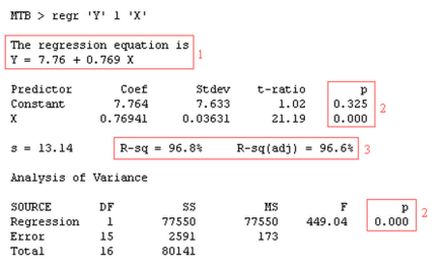
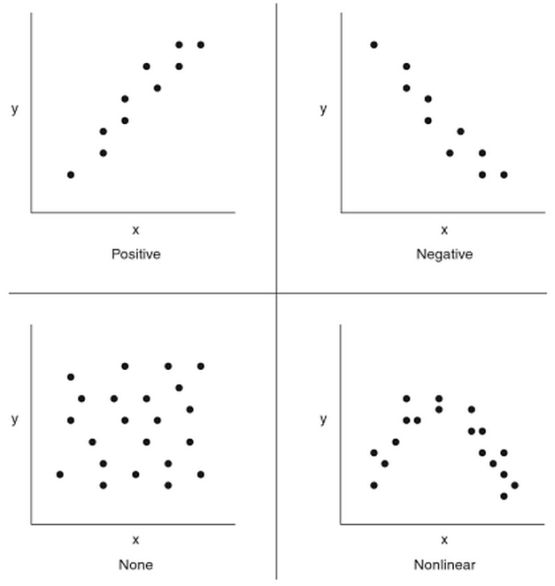
2. Richting: het teken voor de coëfficiënt geeft de richting van het verband aan. Een positief verband tussen variabelen betekent dat hoge waarden op de ene variabele samengaan met hoge waarden van de andere; hetzelfde geld voor lage waarden. Een negatieve correlatie betekent dat hoge waarden op de ene variabele samengaan met lage waarden op de andere variabele. Hoe groter de absolute waarde van de correlatiecoëfficiënt, des te sterker het verband tussen beide variabelen

3. Sterke van het verband: afhankelijk van het soort verband dat wordt onderzocht kan de sterkte van de samenhang tussen twee variabelen worden voorgesteld als sterk, gematigd, zwak of niet-bestaand. De correlatiecoëfficiënt geeft aan in hoeverre de relatie tussen beide variabelen lijkt op een rechte lijn. De sterkte van het verband tussen twee variabelen wordt uitgedrukt in een getal tussen -1 en +1. Een waarde van -1 of +1 duidt erop dat de punten precies op een rechte lijn liggen; er is sprake van een perfect (lineair) verband. Als de correlatiecoëfficiënt 0 is, is er geen sprake van een rechtlijnig verband. Tussenliggende waarden duiden op enig verband tussen de variabelen.

De grootte van de correlatie kan zowel in woorden als getallen beschreven. Correlaties van 0,90 of hoger noemen we meestal 'groot', 'sterk' of 'hoog'. Correlaties van 0,30 of minder noemen we meestal klein, zwak of laag. Correlaties tussen 0,30 en 0,80 noemen we meestal gematigd of bescheiden. Een andere indeling is:

Enkelvoudige lineaire regressie is de meest simpele vorm van regressie heeft als doel het analyseren van een continue, onafhankelijke variabel en een continue, afhankelijke variabele. Bij het onderzoeken van de correlatie tussen twee continue variabelen, wordt geanalyseerd of een continue variabele (Y) door een andere continue variabele (X) wordt verklaard of voorspeld: Y=F(X). De regressievergelijking is de vergelijking die de samenhang weergeeft tussen de afhankelijke variabele en een of meer andere variabelen die haar beïnvloeden (de onafhankelijke variabelen). Met de regressievergelijking is het mogelijk de procesprestatie (Y) te voorspellen bij een specifieke waarde van de variabele X. De vergelijking kan worden gevisualiseerd door middel van een zogenaamde regressielijn die staat voorde lijn waarmee de ligging van een puntenwolk (verzameling van punten die ontstaat als je de meetwaarden van twee variabelen in een assenstelsel tegen elkaar uitzet) kan worden aangeduid.

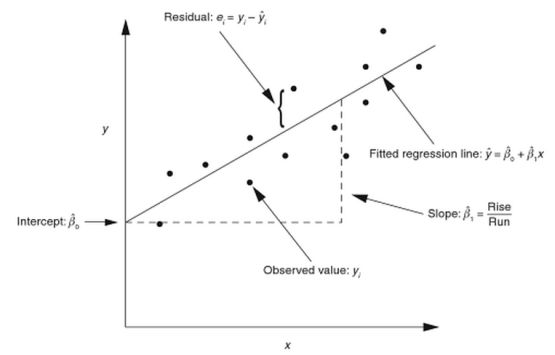
De regressievergelijking staat voor de lineaire functie die in staat is zoveel mogelijk datapunten te verklaren, en de datadeviatie (residuals) van de functie te minimaliseren. Het enkelvoudige lineaire regressiemodel heeft als formule:  Y = a + bx + E (epsilon). Binnen deze formule staat Y voor de afhankelijke variabele, en X voor de onafhankelijke variabele (regressor). De 'a' en 'b' staan voor de regressiecoëfficiënten, waarbij 'a' aangeeft waar de regressielijn de y-as snijdt (ook wel 'axis intercept' of constante genoemd; dit is het snijpunt met de y-as als X=0) en 'b' staat voor de hoek van de regressielijn (hellingsgetal, richtingcoëfficiënt). In de vergelijking staat de E (epsilon) voor de foutvoorwaarde (het residu, ook wel error term; residuals genoemd); 'fout' in de zin dat het gaat om de afwijking tussen de geobserveerde waarde van y en de voorspelde waarde van y. De analyse van residuen op de grafieken biedt belangrijk inzicht over hoe goed het model past. Als de residuen normaal zijn verdeeld, dan liggen ze grofweg op een lijn in een normaliteitsplot plot en de histogram heeft de vorm van een normale verdeling.

Er is sprake van een negatief verband als er een verband bestaat tussen twee variabelen waarbij hoge (lage) waarden van de ene variabele vaak tegelijk optreden met lage (hoge) waarden van de andere. Een positief verband staat voor een verband tussen twee variabelen waarbij hoge (lage) waarden van de ene variabele vaak tegelijk optreden met hoge (lage) waarden van de andere. Bij een 'perfecte' positieve correlatie is de correlatiecoëfficiënt r gelijk aan 1. Bij een 'perfecte' negatieve correlatie is r = -1. Als er geen correlatie is dan r = 0. Dus hoe meer r afwijkt van nul hoe groter de correlatie.

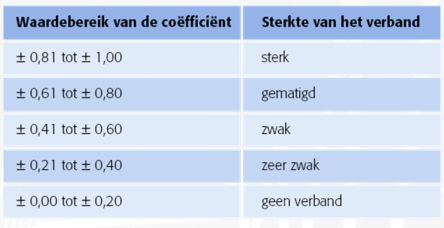
In het bovenstaande voorbeeld is met Minitab een regressie-analyse uitgevoerd, waarbij de correlatie is onderzocht tussen Y en X. Het resultaat kan als volgt

De regressielijn wordt geschat met behulp van de kleinste kwadratenmethode (Gauss): neem die lijn waarvoor de som van de gekwadrateerde residuen zo klein mogelijk is.

Regressievergelijking
Bij (1) zie je de regressievergelijking Y= a + bX, waarbij 'a' = 7,76 en 'b'= 0,769.

Toetsen lineair verband
Het doel van de regressie-analyse is te onderzoeken of de variabele X de variabele Y beïnvloedt. Bij lineaire regressie doe je dit door statistisch te toetsen of de regressie significant is. Concreet houdt dit in dat je toetst of parameter 'b' (de hellingscoëfficiënt) een waarde heeft die significant van 0 verschilt. De nulhypothese is dan ook gelijk aan 'b' = 0 (er is geen lineair verband). De alternatieve hypothese is dat 'b' ongelijk is aan nul (en er dus wél sprake is van een lineair verband). Tot zover de theoretische achtergrond. Als je kijkt naar de gevonden p-waarde (2), is deze lager dan 0,05 en is er (omdat we de nulhypothese verwerpen) reden aan te nemen dat sprake is van een lineair verband.

Determinatiecoëfficiënt
De correlatiecoëfficiënt R is een maat voor de sterkte van het lineaire verband tussen de onafhankelijke variabele Y en de instelvariabele X. De waarde van R ligt altijd tussen -1 en +1 waarbij waarden in de buurt van —1 en +1 een grote lineaire correlatie. Een waarde voor R rond 0 geeft aan dat er geen lineair verband aanwezig is tussen Y en X. In dit voorbeeld is er sprake van en sterk positief lineair verband tussen X en Y.  De 'R-Sq' staat voor R-square, de determinatiecoëfficiënt, die te berekenen is door het kwadrateren van de correlatiecoëfficiënt. R-Sq ligt altijd tussen 0 en 1, omdat R altijd tussen -1 en +1 ligt. De determinatiecoëfficiënt staat voor het aandeel (percentage) van de totale variantie in de ene variabele dat statistisch verklaard wordt door de andere: de verklaarde variantie gedeeld door de totale variantie. Anders gezegd: de determinatiecoëfficiënt (R-sq) geeft aan welk gedeelte van de totale variantie in de afhankelijke variabele Y verklaard wordt door het regressiemodel. 'R-sq (adj)' is de Adjusted R-square: een reëlere schatting van de determinatiecoëfficiënt. Voor de meetgegevens van X en Y wordt dus 99,8 % van de veriantie in Y verklaard door het verkregen lineaire regressiemodel. Goed nieuws: dit wijst erop dat je de belangrijkste invloedsfactor van het proces te gevonden hebt.

In plaats van ons te concentreren op één enkele variabele (univariate regressie-analyse) is het vaak interessant om de relatie te bestuderen tussen een afhankelijke variabelen en meer dan één andere variabelen. In dit geval wordt gesproken van multipele (multivariate) regressieanalyse. Als er een regressielijn opgesteld zou moeten worden, dan zou de volgende algemene formule van toepassing zijn:

y    = a   +   b₁x₁ +   b₂x₂ +   b₃x₃ +    ………. +   b_zx_z

waarbij:
y  = afhankelijke variabele
a  = intercept
b₁ tot b_z = de richting en kracht van de variabele
x₁ tot x_z = de onafhankelijke / voorspellende variabele

De aanpak om te bepalen óf er sprake is van een verband tussen de variabele Y en één of meer van de X'en blijft hetzelfde. In het onderstaande voorbeeld is te zien dat de de variabele x1 wél van invloed is op y, maar dat er geen statistisch significant verband is tussen variabele x2 en Y.

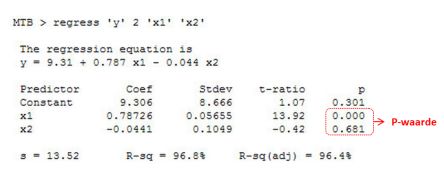
Zoals gezegd is de determinatiecoëfficiënt (R-sq) een maat voor het deel van de variabiliteit dat wordt verklaard door het statistisch model. Er is geen consensus over de exacte definitie van R-sq. Alleen in het geval van lineaire regressie zijn alle definities equivalent. In geval van enkelvoudige lineare regressie is R-sq simpelweg gelijk aan het kwadraat van een correlatiecoëfficiënt. Bij multipel regressie-analyse blijft de R-sq een indicatie van de proportie verklaarde variantie van het regressiemodel, maar is het lastiger dit praktisch te interpreteren.

Bron: The Certified Six Sigma Black Belt Handbook, T. M. Kubiak,Donald W. Benbow