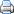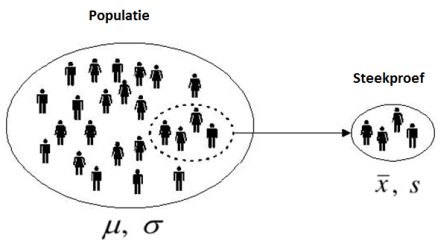
Binnen de (inferentiële) statistiek probeer je vaak op grond van de resultaten van een steekproef conclusies te trekken over de populatie. De populatie is de naam voor de complete groep waarover het statistisch onderzoek gaat. De steekproef is het deel van de populatie dat je bij je onderzoek betrekt. Er zijn twee redenen waarom je gebruik maakt van een steekproef. De eerste is dat de populatie zo groot is dat het onmogelijk is om alle objecten te benaderen. De tweede reden is dat het onderzoek te duur wordt om bij alle objecten metingen te verrichten. Door de inferentiële statistiek toe te passen, is het ook niet noodzakelijk om een hele populatie te bemeten. Ook door slechts een deel van de populatie te bemeten, is de onderzoeker in staat om relevante uitspraken te doen over die populatie.

Bij statistisch onderzoek moet je steeds goed onderscheiden of je over de populatie spreekt dan wel over de steekproef. De populatie is over het algemeen slechts in formele zin gegeven in termen van een kansverdeling met enkele onbekende parameters. Het zijn deze parameters die men graag zou kennen, maar om uiteenlopende redenen niet kent. Een steekproef verschaft informatie over de parameters, door het geven van een schatting, het toetsen van een hypothese over een parameter, e.d. Zo is er het populatiegemiddelde, meestal onbekend, en als schatting daarvan het steekproefgemiddelde. Evenzo is de steekproefvariantie een schatting van de populatievariantie, enzovoorts.

Bij het doen van onderzoek is het - zoals gezegd - zelden mogelijk om alle elementen waarin men geïnteresseerd is (de populatie) te onderzoeken. Je onderzoekt dan een steekproef van elementen uit die populatie. Wil je met enig vertrouwen op basis van een steekproef uitspraken doen over een populatie, dan moet de steekproef representatief en willekeurig (aselect) getrokken zijn. Bij een aselecte steekproef heeft ieder element van de populatie een even grote kans om in de steekproef opgenomen te worden. Uitspraken over populaties zijn altijd kansuitspraken; je weet het nooit helemaal zeker, juist omdat je niet de hele populatie, maar slechts een steekproef onderzocht hebt.

De onafhankelijkheid van steekproeven houdt in dat het trekken van een steekproefelement in de ene steekproef geen invloed heeft op het trekken van elementen in andere steekproeven. De scores in de verschillende steekproeven zijn dan ook onderling onafhankelijk, met andere woorden, alle individuen of observaties in alle steekproeven zijn toevalsgewijs.

In een onderzoek waarin bijvoorbeeld twee groepen van respondenten met elkaar worden vergeleken, en in de éne steekproef enkel mannen zitten, en in de andere enkel de partners van diezelfde mannen, spreek je van afhankelijke of gerelateerde steekproeven. Andere voorbeelden van gerelateerde steekproeven zijn: het afnemen van een vragenlijst bij een aantal personen en het na verloop van een maand afnemen van dezelfde vragenlijst bij dezelfde personen, of het indelen van studenten in twee groepen: een testgroep en een controlegroep. De studenten worden niet toevalsgewijs verdeeld over de test- of controlegroep maar telkens als een student toegewezen wordt aan de testgroep, wordt een andere student met zoveel mogelijk dezelfde  karakteristieken als eerste toegewezen aan de controlegroep (dit is een gepaarde steekproef). Gepaarde waarnemingen zijn meetresultaten bij dezelfde onderzoekseenheid.

Aan een steekproef wordt niet alleen de eis gesteld van representativiteit (= respons is representatief voor de populatie waarover de onderzoeker een uitspraak wil doen), maar gelden ook eisen ten aanzien van de omvang van de steekproef. De steekproef moet voldoende groot zijn om statistisch relevante verbanden en verschillen te vinden maar ook niet te klein om onnodig geld te verspillen.

Aan deze eis kan worden voldaan door vooraf de minimale steekproefomvang te bepalen.

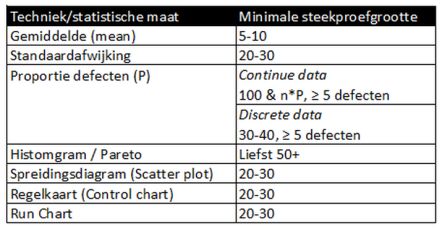
De sterkte van een steekproef (power) wordt getalsmatig beïnvloed door het aantal steekproeven, de waargenomen variatie en het verschil dat waargenomen moet kunnen worden.

Bepalen van de omvang van een steekproef

Voor het bepalen van de steekproefomvang kan gebruik gemaakt worden van de zogenaamde betrouwbaarheidsintervalmethode (confidence interval approach). De methode van het betrouwbaarheidsinterval is een methode, waarbij de begrippen: nauwkeurigheid (steekproeffout), variabiliteit (variability) en het betrouwbaarheidsinterval (confidence interval) worden gecombineerd om een ‘juiste’ steekproefomvang te nemen.

Binnen betrouwbaarheidsintervalmethode staan - zoals gezegd - drie begrippen centraal:

1. Nauwkeurigheid (steekproeffout): het verschil tussen de steekproefuitkomst en de werkelijke populatiewaarde vanwege het feit dat er een steekproef is getrokken.

2. Variabiliteit (variability): Variabiliteit: omschreven als de mate van verschil (of overeenkomst) in de antwoorden van de respondenten op een bepaalde vraag. De variabiliteit wordt berekend door het vermenigvuldigen van p en q, waarbij p staat voor het geschatte percentage in de populatie en q voor het resterende deel van de populatie (100 - p). Hoe groter de variabiliteit, hoe groter de steekproefomvang moet zijn om een bepaalde nauwkeurigheid te bereiken

3. Betrouwbaarheidsinterval (confidence interval): waardegebied waarvan de grenzen een bepaald percentage antwoorden op een vraag omvatten.

Bij het bepalen van de steekproefgrootte wordt uitgegaan van een normale verdeling en de centrale limietstelling.

Bij het bepalen van de steekproefgrootte kun je de normale verdeling gebruiken in verband met de centrale-limietstelling. Ongeacht de vorm van de verdeling van de populatie, zal de verdeling van de steekproeven (als n groter is  dan 30) een normale verdeling aannemen. De eigenschappen van de normale verdeling zijn zodanig dat 1,96 maal de standaardafwijking in theorie de grenzen van 95 procent van de verdeling definieert.

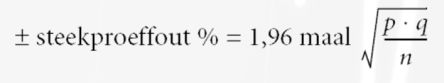
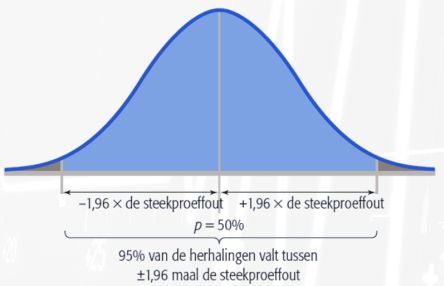
Bij het bepalen van de  juiste steekproefomvang, hoef je slechts drie factoren in overweging te nemen:

1. De (verwachte) mate van variabiliteit in de populatie; bij het bepalen van de variabiliteit in de populatie, geldt als praktische overweging dat je bij het bepalen van de steekproefomvang uitgaat van het slechtste geval(p=50, q=50).

2. De gewenste nauwkeurigheid; bij het vaststellen niveau van de gewenste steekproeffout, geldt dat meestal gegeven is wat een acceptabele steekproeffout is. Vaak is dit +/- 5%. De hoogte van de steekproeffout zal - vanzelfsprekend - afhangen van het belang van de beslissing die op basis van de steekproefresultaten genomen moet worden.

3. Het vereiste betrouwbaarheidsniveau van je schattingen van de populatiewaarden; bij het vaststellen van het gewenste betrouwbaarheidsniveau geldt dat hoe hoger het betrouwbaarheidsniveau moet zijn, des te groter de steekproefomvang wordt. Gebruikelijk is om hiervoor 95% te nemen (z=1,96). Bij een betrouwbaarheidsniveau van 99% hoort een z-waarde van 2,58.

Als het bovenstaande is gespecificeerd, kan op basis van de onderstaande formule de steekproefomvang worden berekend:

Bron: Principes van marktonderzoek,  Alvin C. Burns, Ronald F. Bush, Ingrid Smeets