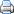
Elke variabele op intervalniveau (en hoger) wordt uitgedrukt op een specifieke schaal. Bijv. de lengte van een persoon uitgedrukt in aantal centimeters. Daarnaast zijn er variabelen die op een 'betekenisloze' schaal worden uitgedrukt. Dit is vaak het geval bij variabelen die opvattingen of gedragingen kwanitificeren, via een 5-puntsschaal.

Soms is het nuttig om variabelen uit te drukken op een schaal die meer betekenis heeft en die dezelfde betekenis heeft voor verschillende variabelen. Een manier om dit te doen is door de variabelen te standaardiseren, hetgeen resulteert in een gestandaardiseerde score. Een veelgebruikte methode voor het standaardiseren is door gebruik te maken van een zogenaamde z-score, ook wel sigmawaarde genoemd.

Als x een waarneming is uit een verdeling van een variabele X met een gemiddelde mu en een standaardafwijking (sigma) dan is de gestandaardiseerde score (z) voor deze waarneming: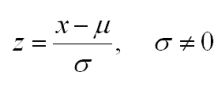


Om een z-score te berekenen trek je dus eerst de gemiddelde score af van elke waarneming en deel je dit resultaat door de standaardafwijking.

Hoe kan je de z-scores interpreteren? Deze z-scores zijn uitgedrukt op een schaal die aangeeft hoeveel standaardafwijkingen een waarneming verwijderd is van het gemiddelde. Meer concreet: een waarneming met een z-score 0 scoort gemiddeld op het waargenomen kenmerk. Een waarneming met een z-score 1 scoort 1 x de standaardafwijking hoger dan het gemiddelde. Een waarneming met een z-score -1, scoort 1 standaardafwijking lagerdan gemiddeld.

Bij variabelen die (bij benadering) normaal verdeeld zijn kan je vervolgens op basis van deze z-scores ook de 68-95-99,7-regel toepassen.

• gemiddelde score (mu) ± standaardafwijking (sigma) is 0,68269 (68%)
• gemiddelde (mu) ± 1,96 x standaardafwijking (sigma) is 0,95450 (95%)  [1,96 wordt meestal afgrond op 2]
• gemiddelde (mu) ± 3 x standaardafwijking (sigma) is 0,99730 (99,7%)

Het betrouwbaarheidsinterval geeft aan tussen welke waarden een onderzoeksuitkomst waarschijnlijk zal zitten. Om vanuit een resultaat uit een steekproef iets over de populatie te zeggen, hou je  een betrouwbaarheidsmarge aan. Deze wordt meestal op 95% gezet, maar je kan ook een betrouwbaarheidsinterval wensen van 99% of van 90%. Omdat je niet weet of het steekproefresultaat naar onderen of naar boven afwijkt, bereken je altijd een onderste en een bovenste waarde. Bij de 68-95-99,7-regel zag je dat bij een betrouwbaarheidsinterval van 95% een z-score 1,96 hoort. Anders gezegd: het 95% betrouwbaarheidsinterval omvat bij een normale verdeling het gebied tussen de z-score van –1,96 en +1,96. 2,5% van de observaties heeft een waarde die ligt onder 1,96 x de standaardafwijking en 2,5% ligt boven 1,96 x de standaardafwijking.

Via onderstaande video-tutorial krijg je een uitgebreide uitleg voor het berekenen van z-waarden:

De berekening van de z-score kan zowel worden gebruikt in de Measure-fase als de Control-fase. In de Measure-fase bereken je de z-score bij wijze van nulmeting (baseline). In de Control-fase bereken je de z-score opnieuw om te bepalen of er verbetering te zien is.

Bron: Openleerpakket beschrijvende statistiek, Sven De Maeyer en Dimokritos Kavadias