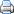
![]()
Mann-Whitney toets
De Mann-Whitney toets is een verdelingsvrije is een verdelingsvrije techniek die gebruikt wordt om na te gaan of twee onafhankelijke variabelen uit dezelfde populatie afkomstig zijn. De toets is voornamelijk gevoelig voor verschillen tussen de gemiddelden van de populaties; in de praktijk komt dit erop neer dat de Mann-Whitney toets gebruikt wordt om de veronderstelling te toetsen dat beide groepen hetzelfde gemiddelde hebben. Als zodanig kan de Mann-Whitney toets gebruikt worden in dezelfde situaties als een t-toets voor het verschil tussen twee gemiddelden. Anders dan bij een t-toets, wordt echter niet verondersteld dat beide populverdelingen normaal verdeeld zijn en dezelfde spreiding bezitten.
Bij de Mann-Whitney toets ordent men de waarnemingen uit beide steekproeven, ongeacht de steekproef waaruit de waarnemingen afkomstig zijn, van laag naar hoog. De laagste score krijgt rangnummer 1, de daarop volgende score krijgt rangnummer 2, enzovoort. Laten we beide groepen aanduiden als A en B. Als nu de ene groep duidelijker lagere resultaten behaalt dan de andere, levert dit veel lage rangummers op. De mensen uit de ene groep (stel dat dit A is) zitten vooral 'voorin' de rangschikking, veel mensen uit de andere groep (B) zitten achterin. Anders gezegd: er zullen veel A's voorafgaan aan de B's.
Als er daarentegen geen wezenlijk verschil tussen de groepen bestaat, zal de volgorde van A's en B's willekeurig zijn: er zal even vaak een A voorafgaan aan B als omgekeerd.
(...)
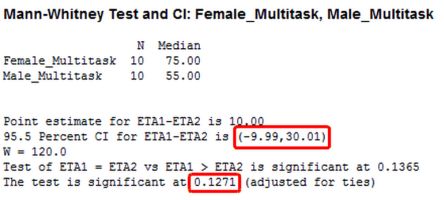
Het wezen van een Mann-Whitney toets bestaat erin, te tellen hoeveel B's er vooraf gaan aan iedere A. De eerste A (score 18) staat in de rangschikking op de vijfde plaats, er gaan 4 B's aan vooraf. De tweede A (op de zesde plaats) wordt eveneens door 4 B's voorafgegaan. De derde A (plaats 8) wordt voorafgegaan door 5 B's, enzovoort. In totaal 4 + 4 + 5 + 5 +5 +5 = 28. Men noemt dit getal U. Men kan ook tellen hoeveel A's er voorafgaan aan iedere B; dit noemt men U'. U' is hier 0 + 0 + 0 + 0 + 2 = 2.
Als de groepen niet wezenlijk van elkaar verschillen, moet U' gelijk zijn aan U. In dat geval verwachten we immers een willekeurige verdeling van A's en B's; er zal dan even vaak een A voorafgaan aan een B als omgekeerd. Hoe groter het verschil tussen U' en U, des te meer reden er is om aan te nemen dat de groepsgemiddelden wèl van elkaar verschillen. Met behulp van tabellen kan getoetst worden of het verschil significant (dit is: niet op toeval berustend) is.
De Mann-Whitney toets is oorspronkelijk bedacht door Wilcoxon en verder ontwikkeld door de heren Mann en Whitney. Men komt hier een daar de toets nog tegen onder de naam Wilcoxoon-toets voor twee onafhankelijke steekproeven.
Omdat de gebruikte toetststatiek U genoemd wordt, spreekt men ook wel van de U-toets van Mann-Whitney.
![]()
Mann-Whitney U-toets
De Mann-Whitney U-toets wordt gebruikt voor het berekenen van een verschil in de rangorde van twee groepen op een variabele.
Bijvoorbeeld, in een wedstrijd tussen twee landen zijn de turners van land A geëindigd op de 1ste, 2e, 6e, 7e en in land B op de 3e, 4e, 5e, 8e, plaats. Welk land is gemiddeld genomen beter? Men zegt dat er geen verschil is als de som van de rangorde getallen in de ene groep net zo hoog als in de andere groep (onder de voorwaarde dat de groepen evengroot zijn). Om te toetsen of de som van de rangorde getallen groter is in de ene groep dan in de andere, berekent men de Mann-Whitney U-waarde
![]()
Mann-Whitney U-toets
Bij variabelen op ordinaal meetniveau kun je berekenen of de mediaan van de variabele tussen de groepen significant verschilt. Je wilt bijvoorbeeld weten of personeelsleden van de ene afdeling significant verschillen van de personeelsleden van een andere afdeling in de beoordeling die ze van hun baas hebben gekregen. De beoordeling is gegeven op een vierpuntsschaal (zwaar onvoldoende - onvoldoende - voldoende - goed). Je kunt met de Mann-Whitney U-toets berekenen of de ene afdeling significant hoger scoort dan de andere. Bij P <= alpha mag je aannemen dat de groepen significant verschillen.
Bron: