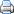A.W. Alings beschrijft op archaïsche wijze - maar niet minder treffend - wat meten is:

Opdat men in 't algemeen, ook zonder onmiddellijk aanschouwing, zich gemakkelijk zal kunnen voorstellen, hoe groot ene zekere grootheid is, wordt alleen vereischt, dat men de uitkomst kent ter vergelijking van die grootheid met eene andere grootheid, welke grootte goed bekend is. Deze laatste grootheid wordt dan de eenheid of maat genoemd; het onderzoek dat leert, hoe dikwijls die eenheid of een bepaald deel daarvin in de gegevene grootheid begrepen is, heet meten.

(...)

Wanneer de gebezigde eenheid een geheel aantal malen, b.v. 5 malen, in de gegevene grootheid bevat is, dan zegt men, dat deze grootheid gelijk is aan 5 van die grootheden, elk gelijk aan die eenheid. Indien niet de geheele eenheid, maar wel een evenmatig deel daarvan, b.v. een zevendedeel, een geheel aantal malen, b.v. 3 of 15 malen, in de gegevene grootheid begrepen is, dan zegt men, dat deze grootheid gelijk is aan 3/7 of aan 2 1/7 eenheid.

Bron: Beginselen der rekenkunde (Volume 2), Arnoldus Wilhelm Alings